Numbering Systems and Compute

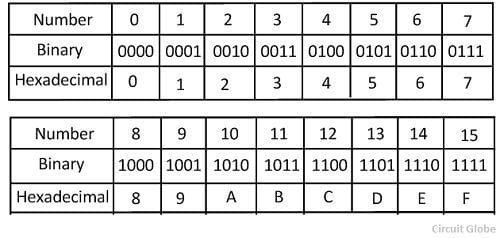
In the world of computation, we should have a firm understanding of how machines compute data and bits of information. This means being familiar with the numbering systems commonly used today, which systems are used by computers, and how they relate to each other.

The three common numbering systems used are Decimal, Binary and Hexadecimal, with decimal being our commonly used counting system, binary being used in computation and hexadecimal being used to make it easier to read long strings of binary.

The Decimal (Base 10) Numbering System

• To understand the Binary (Base 2) and Hexadecimal (Base 16) numbering systems used in computing, we should first seek to understand the Decimal (Base 10) numbering system used in everyday calculations.

• The term Base refers to the number of unique symbols used to represent numbers. In the Decimal (Base 10) system, we use the digits 0,1, 2 etc through to 9, equating to 10 digits.

• If we take any number as an example, let’s say 163, and give each digit in this a “position” from left to right, then 1 would be in position 2, 6 would be in position 1 and 3 would be in position 0.

• We can use the digits of 163, their positions as outlined above and the number 10 and as a multiplier to get back to the number 163.

• Starting with the number 1 in position 2, we would multiply it by 10 to the power of its position which is 2 (1x10² ). To this we would add 6 multiplied by 10 to the power of 1 (6x10¹ ) and to this we would add 3 multiplied by 10 to the power of 0 (3x10⁰ ).

• Written out and solved this looks like the following:
  (1x10² ) + (6x10¹ ) + (3x10⁰ )
  (1x100) + (6x10) + (3x1)
  100 + 60 + 3 = 163

The Binary (Base 2) System

• When we start talking about the binary system, we refer to it as Base 2 because there are only 2 unique ways to represent numbers, these being 0 and 1. In compute, these 0s and 1s are used to represent the on/off states of electrical switches, with 0 being off and 1 being on.

• If we take the prior example of the number 163, in binary it is represented as 10100011. Why this is will become clear soon however we can take this string of binary numbers and using the same system as before (swapping out 10 for 2 but keeping the positions of each digit as the superscripts), we can work back to the number 163

• Starting from left to right and working down to position 0, we can see that in 10100011 the first 1 is in position 7, the proceeding 0 is in position 6, then 1 in position 5, then 3 0s each in positions 4, 3, and 2 respectively, followed by a 1 in position 1 and a 1 in position 0.

• In this example, when calculating our way back to 163 we can disregard the 0s as they will result in 0 and won’t have a bearing on our calculation. That leaves us with the 1s in positions 7, 5, 1 and 0 that we will calculate in that order

• Using the same rules as before where our exponents are the positions of our respective numbers in the binary series, the 1 in position 7 would be multiplied by 2⁷ , the next 1 in position 5 by 2⁵ , then 1 by 2¹ and lastly 1 by 2⁰ .

• Written out and solved is as follows:
  (1x2⁷ ) + (1x2⁵ ) + (1x2¹ ) + (1x2⁰ )
  (1x128) + (1x32) + (1x2) +(1x1)
  128 + 32 + 2 + 1 = 163

• Numbers in a binary series are called bits, and each bit, going from right to left, is represented by 2 to the power of the position of the bit, starting at 0 and increasing by 1 each time.

• In a 5 bit series, let’s say 11010, the first 0 on the right is 2⁰ , the 1 after it is 2¹ , the 0 after that is 2² , and the remaining ones in the series are 2³ and 2⁴ respectively

• This means these bits, from right to left, would have the values 1, 2, 4, 8, and 16 individually, however if we wanted to know what the full binary series sums to in decimal we have to think of back to the 0 representing off and the 1 representing on.

• 0 (off) multiplied by 1 is 0, and 0 (off) multiplied by 4 is 0

• Calculating this back into decimal based on these on and off switches would mean that we have the following calculation:

• (1x16) + (1x8) + (0x4) + (1x2) + (0x1)

• 16 + 8 + 0 + 2 + 0 = 26

• This means this binary series 11010 = 26 in decimal.

• An easy way to remember what the bits in a binary series represent is to continue and remember the sequence of 2 with the exponents 0, 1, 2 etc increasing by 1 each time, which would be 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096 and so forth and so on.

Hexadecimal (Base 16) System

• The Hexadecimal System is used primarily in computer science to represent binary data in an easier to read format.

• The formula for converting a hexadecimal number back to decimal is the same as for our previous two numbering systems. We multiply the number we wish to convert by the base (16 in this case) which has the exponent as the position of the converting number in the hexadecimal series.

• Before we convey this with our example of 163, we should seek to understand how numbers are represented in the hexadecimal system. We have first 9 numbers just like the decimal system, 0-9. After this we use letters starting from A to represent numbers 10 and up. A =10, B=11, C=12, D=13, E=14, F=15

• 163 written out as hexadecimal as A3

• From right to left, 3 is in position 0 and A is in position 1

• A represents 10, and 3 represents 3

• Therefore, to get to 163 we do the following calculation:

• (10x16¹ ) + (3x16⁰ )

• (10x16) + (3x1)

• 160 + 3 = 163